In this post, we will explore the use of generalization gap modeling for hyperparameter optimization of a LightGBM model. A surrogate model (here a kernel ridge regression model) is fitted on the gap between a model’s cross-validation error and test set error. Our surrogate model could then be used to predict the generalization gap for new hyperparameter combinations, and obtain various insights on the LightGBM model’s ability to generalize on unseen data.

More details can be found in this document https://www.researchgate.net/publication/398667338_Beyond_Performance_Hyperparameter_Optimization_via_Direct_Generalization_Gap_Modeling.

install.packages("pak")

pak::pak(c("caret", "lightgbm", "KRLS", "dplyr"))

pak::pak("gridExtra")

# ==================== COMPLETE R IMPLEMENTATION ====================
# Load required libraries
library(MASS)
library(caret)
library(lightgbm)
library(KRLS)
library(dplyr)
library(ggplot2)

# Set seed for reproducibility
set.seed(2026)

# Load and prepare Boston dataset
data(Boston)
Boston <- as.data.frame(Boston)

# Define the target variable and features
target_var <- "medv"
features <- setdiff(names(Boston), target_var)

# Split dataset into training (70%) and test (30%) sets
train_index <- caret::createDataPartition(Boston[[target_var]], p = 0.7, list = FALSE)
train_data <- Boston[train_index, ]
test_data <- Boston[-train_index, ]

# Define hyperparameter grid for LightGBM (could be a Sobol sequence)
n <- 200
set.seed(123)
hyper_grid <- data.frame(
  num_leaves = sample(c(15, 31, 45), n, replace = TRUE),
  learning_rate = runif(n, 0.01, 0.1),
  n_estimators = sample(c(50, 100, 150), n, replace = TRUE),
  max_depth = sample(c(-1, 5, 10), n, replace = TRUE),
  min_data_in_leaf = sample(c(20, 50, 100), n, replace = TRUE),
  feature_fraction = runif(n, 0.7, 0.9)
)

# Initialize results table
results_table <- data.frame()

cat("Training LightGBM models...\n")

# Train LightGBM models with different hyperparameter combinations
for(i in 1:min(30, nrow(hyper_grid))) {
  cat(paste("Training model", i, "of", min(30, nrow(hyper_grid)), "...\n"))

  # Get current hyperparameters
  current_params <- hyper_grid[i, ]

  # Create LightGBM dataset
  lgb_train <- lgb.Dataset(
    data = as.matrix(train_data[, features]),
    label = train_data[[target_var]]
  )

  # Set up 5-fold cross-validation
  cv_folds <- 5
  cv_results <- lgb.cv(
    params = list(
      objective = "regression",
      metric = "rmse",
      num_leaves = current_params$num_leaves,
      learning_rate = current_params$learning_rate,
      max_depth = current_params$max_depth,
      min_data_in_leaf = current_params$min_data_in_leaf,
      feature_fraction = current_params$feature_fraction,
      verbose = -1
    ),
    data = lgb_train,
    nrounds = current_params$n_estimators,
    nfold = cv_folds,
    eval_freq = 50,
    early_stopping_rounds = 20,
    stratified = FALSE
  )

  # Get best CV score
  cv_best_score <- min(as.numeric(cv_results$record_evals$valid$rmse$eval))
  cv_best_iter <- cv_results$best_iter #which.min(as.numeric(cv_results$record_evals$valid$rmse$eval))

  # Train final model on full training data
  final_model <- lgb.train(
    params = list(
      objective = "regression",
      metric = "rmse",
      num_leaves = current_params$num_leaves,
      learning_rate = current_params$learning_rate,
      max_depth = current_params$max_depth,
      min_data_in_leaf = current_params$min_data_in_leaf,
      feature_fraction = current_params$feature_fraction,
      verbose = -1
    ),
    data = lgb_train,
    nrounds = cv_best_iter
  )

  # Predict on test set
  test_pred <- predict(final_model, as.matrix(test_data[, features]))

  # Calculate test RMSE
  test_rmse <- sqrt(mean((test_pred - test_data[[target_var]])^2))

  # Calculate gap
  gap <- cv_best_score - test_rmse

  # Add to results table
  results_table <- rbind(results_table,
                         data.frame(
                           model_id = i,
                           num_leaves = current_params$num_leaves,
                           learning_rate = current_params$learning_rate,
                           n_estimators = current_params$n_estimators,
                           max_depth = current_params$max_depth,
                           min_data_in_leaf = current_params$min_data_in_leaf,
                           feature_fraction = current_params$feature_fraction,
                           cv_rmse = cv_best_score,
                           test_rmse = test_rmse,
                           gap = gap
                         )
  )
}

# Display final results table
cat(paste("\n", paste(rep("=", 80), collapse = ""), "\n"))
cat("FINAL RESULTS TABLE\n")
cat(paste(rep("=", 80), collapse = ""), "\n")
print(results_table)

# Save results to CSV
write.csv(results_table, "lightgbm_results_r.csv", row.names = FALSE)

# ==================== KRLS MODELING ====================
cat(paste("\n", paste(rep("=", 80), collapse = ""), "\n"))
cat("KRLS MODEL DIAGNOSTICS\n")
cat(paste(rep("=", 80), collapse = ""), "\n")

# Prepare data for KRLS modeling
krls_X <- results_table[, c("num_leaves", "learning_rate", "n_estimators",
                            "max_depth", "min_data_in_leaf", "feature_fraction")]
krls_y <- results_table$gap

# Fit KRLS model on the gap
cat("\nFitting KRLS model...\n")
krls_model <- krls(
  X = krls_X,
  y = krls_y,
  derivative = TRUE,
  whichkernel = "gaussian",
  lambda = NULL,
  sigma = NULL
)

# 1. Model Summary
cat("\n1. MODEL SUMMARY:\n")
print(summary(krls_model))

# 2. Optimal hyperparameters
cat("\n2. OPTIMAL HYPERPARAMETERS:\n")
cat("   Lambda (regularization):", krls_model$lambda, "\n")
cat("   Sigma (kernel bandwidth):", krls_model$sigma, "\n")

# 3. Model Fit Statistics
cat("\n3. MODEL FIT STATISTICS:\n")
print(krls_model)

# 4. Partial Derivatives (Marginal Effects)
cat("\n4. PARTIAL DERIVATIVES (Average Marginal Effects):\n")
partial_derivs <- colMeans(krls_model$derivatives)
names(partial_derivs) <- colnames(krls_X)
print(partial_derivs)


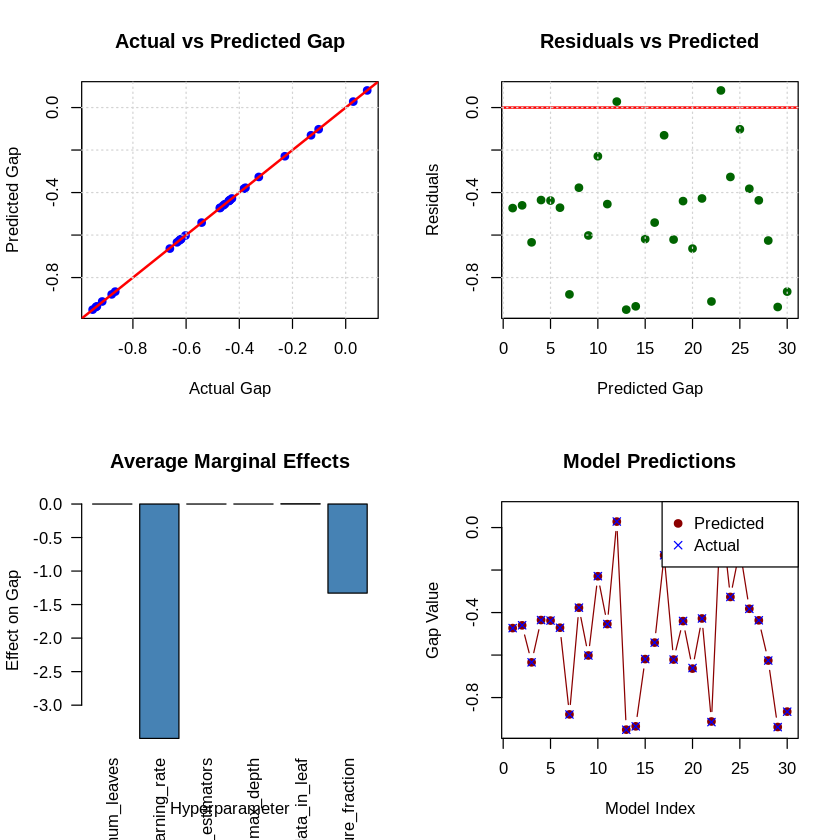
# 6. Diagnostic Plots
cat("\n6. GENERATING DIAGNOSTIC PLOTS...\n")

par(mfrow = c(2, 2))

# Plot 1: Actual vs Predicted
plot(krls_y, krls_model$fitted,
     main = "Actual vs Predicted Gap",
     xlab = "Actual Gap",
     ylab = "Predicted Gap",
     pch = 19, col = "blue")
abline(0, 1, col = "red", lwd = 2)
grid()

# Plot 2: Residuals vs Predicted
plot(krls_model$fitted, krls_model$residuals,
     main = "Residuals vs Predicted",
     xlab = "Predicted Gap",
     ylab = "Residuals",
     pch = 19, col = "darkgreen")
abline(h = 0, col = "red", lwd = 2)
grid()

# Plot 5: Marginal effects (bar plot)
barplot(partial_derivs,
        main = "Average Marginal Effects",
        xlab = "Hyperparameter",
        ylab = "Effect on Gap",
        col = "steelblue",
        las = 2)

# Plot 6: Learning curve
plot(krls_model$fitted, type = "b",
     main = "Model Predictions",
     xlab = "Model Index",
     ylab = "Gap Value",
     col = "darkred", pch = 19)
points(krls_y, col = "blue", pch = 4)
legend("topright", legend = c("Predicted", "Actual"),
       col = c("darkred", "blue"), pch = c(19, 4))

cat("   Diagnostic plots saved to 'krls_diagnostics_r.png'\n")

# 7. Create summary plots of the gap vs hyperparameters
cat("\n7. GAP ANALYSIS BY HYPERPARAMETER:\n")

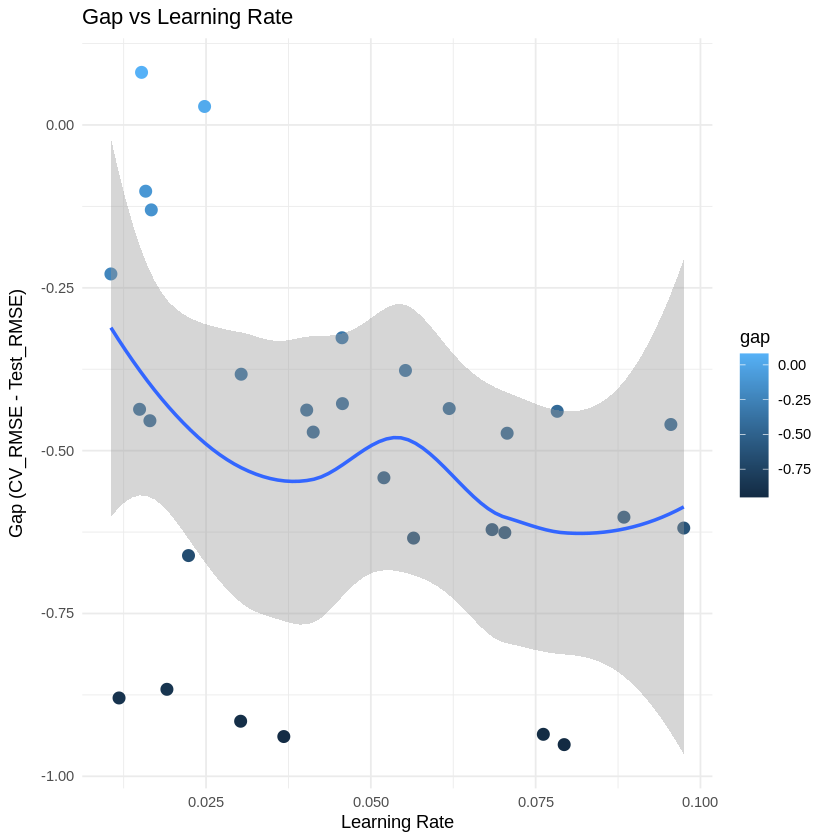
# Plot gap vs learning rate
p1 <- ggplot(results_table, aes(x = learning_rate, y = gap)) +
  geom_point(aes(color = gap), size = 3) +
  geom_smooth(method = "loess", se = TRUE) +
  labs(title = "Gap vs Learning Rate",
       x = "Learning Rate",
       y = "Gap (CV_RMSE - Test_RMSE)") +
  theme_minimal()
print(p1)
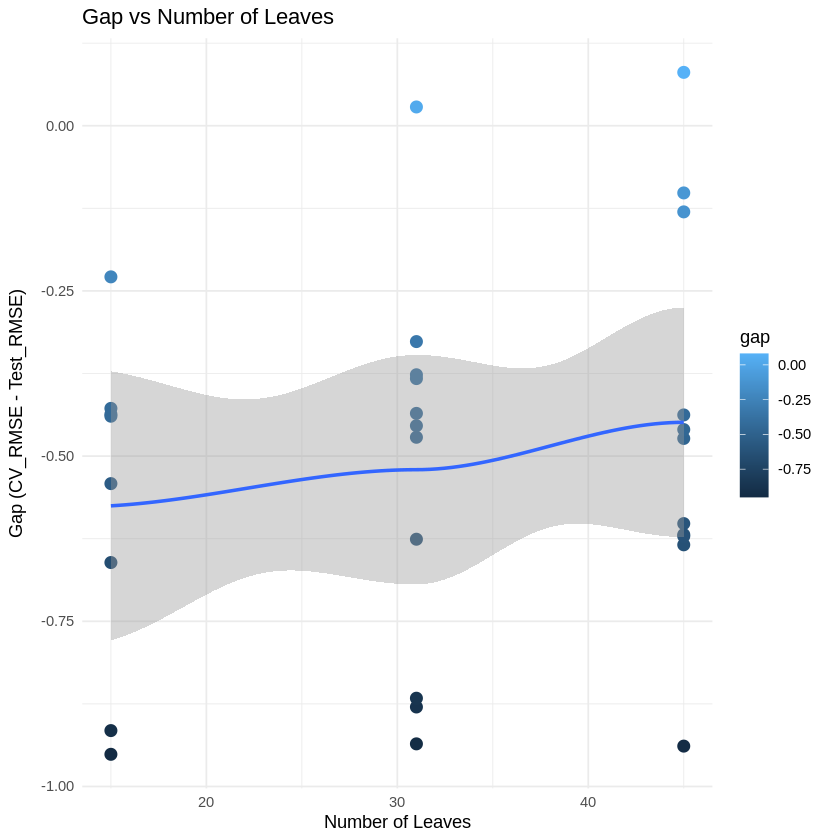
# Plot gap vs num_leaves
p2 <- ggplot(results_table, aes(x = num_leaves, y = gap)) +
  geom_point(aes(color = gap), size = 3) +
  geom_smooth(method = "loess", se = TRUE) +
  labs(title = "Gap vs Number of Leaves",
       x = "Number of Leaves",
       y = "Gap (CV_RMSE - Test_RMSE)") +
  theme_minimal()
print(p2)
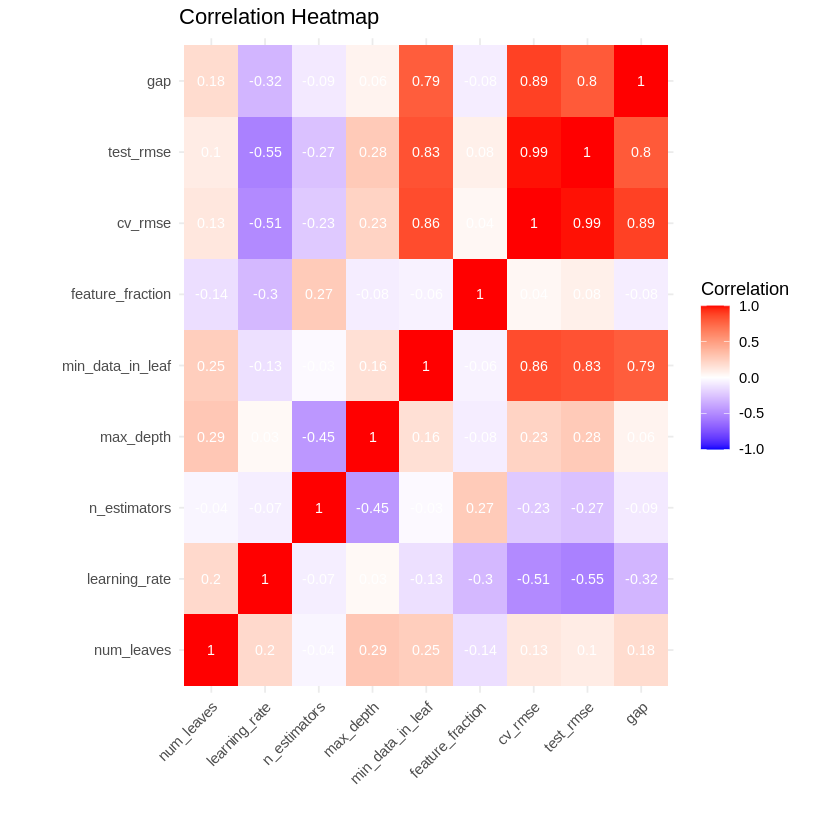
# Plot correlation heatmap
cor_matrix <- cor(results_table[, c("num_leaves", "learning_rate", "n_estimators",
                                    "max_depth", "min_data_in_leaf", "feature_fraction",
                                    "cv_rmse", "test_rmse", "gap")])

p3 <- ggplot(data = reshape2::melt(cor_matrix),
             aes(x = Var1, y = Var2, fill = value)) +
  geom_tile() +
  geom_text(aes(label = round(value, 2)), color = "white", size = 3) +
  scale_fill_gradient2(low = "blue", high = "red", mid = "white",
                       midpoint = 0, limit = c(-1, 1), space = "Lab") +
  labs(title = "Correlation Heatmap",
       x = "", y = "", fill = "Correlation") +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))
print(p3)
# Save gap analysis plots
ggsave("gap_analysis_plots_r.png",
       gridExtra::arrangeGrob(p1, p2, p3, ncol = 2),
       width = 12, height = 8, dpi = 300)
cat("   Gap analysis plots saved to 'gap_analysis_plots_r.png'\n")

# 8. Find best hyperparameters (lowest gap)
cat("\n8. BEST HYPERPARAMETER CONFIGURATIONS:\n")

# Sort by gap (lowest gap = best generalization)
sorted_results <- results_table[order(abs(results_table$gap)), ]

# Top 3 best configurations
cat("\nTop 3 configurations with smallest gap (best generalization):\n")
for(i in 1:min(3, nrow(sorted_results))) {
  cat(paste("\nRank", i, ":\n"))
  cat("  Gap:", sorted_results$gap[i], "\n")
  cat("  CV RMSE:", sorted_results$cv_rmse[i], "\n")
  cat("  Test RMSE:", sorted_results$test_rmse[i], "\n")
  cat("  num_leaves:", sorted_results$num_leaves[i], "\n")
  cat("  learning_rate:", sorted_results$learning_rate[i], "\n")
  cat("  n_estimators:", sorted_results$n_estimators[i], "\n")
  cat("  max_depth:", sorted_results$max_depth[i], "\n")
  cat("  min_data_in_leaf:", sorted_results$min_data_in_leaf[i], "\n")
  cat("  feature_fraction:", sorted_results$feature_fraction[i], "\n")
}

# Worst 3 configurations (largest gap = most overfitting)
sorted_results_worst <- results_table[order(-abs(results_table$gap)), ]
cat("\n\nTop 3 configurations with largest gap (most overfitting):\n")
for(i in 1:min(3, nrow(sorted_results_worst))) {
  cat(paste("\nRank", i, ":\n"))
  cat("  Gap:", sorted_results_worst$gap[i], "\n")
  cat("  CV RMSE:", sorted_results_worst$cv_rmse[i], "\n")
  cat("  Test RMSE:", sorted_results_worst$test_rmse[i], "\n")
  cat("  num_leaves:", sorted_results_worst$num_leaves[i], "\n")
  cat("  learning_rate:", sorted_results_worst$learning_rate[i], "\n")
  cat("  n_estimators:", sorted_results_worst$n_estimators[i], "\n")
  cat("  max_depth:", sorted_results_worst$max_depth[i], "\n")
  cat("  min_data_in_leaf:", sorted_results_worst$min_data_in_leaf[i], "\n")
  cat("  feature_fraction:", sorted_results_worst$feature_fraction[i], "\n")
}

# 9. Statistical analysis of gap
cat("\n9. STATISTICAL ANALYSIS OF GAP:\n")
cat("   Mean gap:", mean(results_table$gap), "\n")
cat("   Standard deviation:", sd(results_table$gap), "\n")
cat("   Minimum gap:", min(results_table$gap), "\n")
cat("   Maximum gap:", max(results_table$gap), "\n")
cat("   Median gap:", median(results_table$gap), "\n")

# Test if gap is significantly different from zero
t_test <- t.test(results_table$gap)
cat("   t-test for gap = 0: t =", t_test$statistic,
    ", p-value =", t_test$p.value, "\n")
if(t_test$p.value < 0.05) {
  cat("   Conclusion: Gap is significantly different from zero (p < 0.05)\n")
} else {
  cat("   Conclusion: Gap is not significantly different from zero\n")
}

cat("overfitting?")
(t_test2 <- t.test(results_table$gap, alternative = "greater"))

cat("underfitting?")
(t_test3 <- t.test(results_table$gap, alternative = "less"))

# 10. Save KRLS model
saveRDS(krls_model, "krls_model_r.rds")
cat("\n10. KRLS model saved to 'krls_model_r.rds'\n")

cat(paste("\n", paste(rep("=", 80), collapse = ""), "\n"))
cat("ANALYSIS COMPLETE\n")
cat("Results saved to:\n")
cat("  - lightgbm_results_r.csv: LightGBM hyperparameter results\n")
cat("  - krls_model_r.rds: KRLS model object\n")
cat("  - krls_diagnostics_r.png: KRLS diagnostic plots\n")
cat("  - gap_analysis_plots_r.png: Gap analysis visualizations\n")
cat(paste(rep("=", 80), collapse = ""), "\n")

# Print completion message
cat("\n✅ All R code executed successfully!\n")


Training LightGBM models...
Training model 1 of 30 ...
Training model 2 of 30 ...
Training model 3 of 30 ...
Training model 4 of 30 ...
Training model 5 of 30 ...
Training model 6 of 30 ...
Training model 7 of 30 ...
Training model 8 of 30 ...
Training model 9 of 30 ...
Training model 10 of 30 ...
Training model 11 of 30 ...
Training model 12 of 30 ...
Training model 13 of 30 ...
Training model 14 of 30 ...
Training model 15 of 30 ...
Training model 16 of 30 ...
Training model 17 of 30 ...
Training model 18 of 30 ...
Training model 19 of 30 ...
Training model 20 of 30 ...
Training model 21 of 30 ...
Training model 22 of 30 ...
Training model 23 of 30 ...
Training model 24 of 30 ...
Training model 25 of 30 ...
Training model 26 of 30 ...
Training model 27 of 30 ...
Training model 28 of 30 ...
Training model 29 of 30 ...
Training model 30 of 30 ...

 ================================================================================ 
FINAL RESULTS TABLE
================================================================================ 
   model_id num_leaves learning_rate n_estimators max_depth min_data_in_leaf
1         1         45    0.07067682          100        10              100
2         2         45    0.09551503           50        10               50
3         3         45    0.05648004          150        -1               20
4         4         31    0.06188671          100        10              100
5         5         45    0.04026981          150        10              100
6         6         31    0.04125922          100        -1              100
7         7         31    0.01180219          150         5               20
8         8         31    0.05525317          150        -1              100
9         9         45    0.08839391           50         5               50
10       10         15    0.01056707          100         5               50
11       11         31    0.01648514          150        -1               50
12       12         31    0.02477901           50        10              100
13       13         15    0.07933007           50        -1               20
14       14         31    0.07616659          150         5               20
15       15         45    0.09746881          100         5               50
16       16         15    0.05198251          150        -1               50
17       17         45    0.01669461          100         5              100
18       18         45    0.06839363          100        -1               50
19       19         15    0.07827339          100        -1               50
20       20         15    0.02233955           50         5               20
21       21         15    0.04569261          100         5              100
22       22         15    0.03024868           50         5               20
23       23         45    0.01521627           50         5              100
24       24         31    0.04563034           50        10              100
25       25         45    0.01584355          100        -1              100
26       26         31    0.03032978          100        -1              100
27       27         15    0.01491662          150        -1               50
28       28         31    0.07032538          150        -1               50
29       29         45    0.03679676           50        10               20
30       30         31    0.01906494          100         5               20
   feature_fraction  cv_rmse test_rmse         gap
1         0.8246258 5.494526  5.967797 -0.47327065
2         0.7622057 4.405432  4.865283 -0.45985065
3         0.7784393 3.508353  4.142610 -0.63425683
4         0.7404175 5.592263  6.027616 -0.43535302
5         0.8705561 5.565326  6.003025 -0.43769840
6         0.8213660 5.619463  6.090962 -0.47149897
7         0.8512196 4.144238  5.023945 -0.87970718
8         0.8125034 5.592810  5.969701 -0.37689099
9         0.7551798 4.306615  4.908771 -0.60215595
10        0.8471117 5.816231  6.044941 -0.22871041
11        0.8098560 4.809378  5.263431 -0.45405362
12        0.7692254 6.704490  6.676068  0.02842218
13        0.8029931 3.585176  4.536517 -0.95134165
14        0.8631536 3.232667  4.168185 -0.93551740
15        0.8052545 4.107878  4.726707 -0.61882871
16        0.7406080 4.294992  4.836629 -0.54163683
17        0.8696215 6.304009  6.434366 -0.13035745
18        0.7740988 4.209949  4.831197 -0.62124727
19        0.7606650 4.308604  4.748225 -0.43962106
20        0.8541194 4.936170  5.597256 -0.66108664
21        0.8466897 5.629371  6.057179 -0.42780729
22        0.8677812 4.276730  5.192173 -0.91544349
23        0.8138098 7.269937  7.189151  0.08078594
24        0.7052562 6.003408  6.330080 -0.32667215
25        0.7972254 6.372935  6.474612 -0.10167741
26        0.8085362 5.826914  6.209579 -0.38266514
27        0.8673320 4.877480  5.314011 -0.43653105
28        0.8457329 4.065288  4.691104 -0.62581641
29        0.8110228 3.989341  4.928279 -0.93893733
30        0.7146829 4.122488  4.988929 -0.86644109

 ================================================================================ 
KRLS MODEL DIAGNOSTICS
================================================================================ 

Fitting KRLS model...


Warning message in Eigenobject$values + lambda:
“Recycling array of length 1 in vector-array arithmetic is deprecated.
  Use c() or as.vector() instead.”
Warning message in Eigenobject$values + lambda:
“Recycling array of length 1 in vector-array arithmetic is deprecated.
  Use c() or as.vector() instead.”



 Average Marginal Effects:
 
      num_leaves    learning_rate     n_estimators        max_depth 
   -0.0006775316    -3.4958642058     0.0001547258     0.0000539840 
min_data_in_leaf feature_fraction 
    0.0036386780    -1.3287593021 

 Quartiles of Marginal Effects:
 
       num_leaves learning_rate  n_estimators    max_depth min_data_in_leaf
25% -0.0060738302     -6.370737 -0.0013469621 -0.011036161      0.002516728
50%  0.0006160114     -3.803870 -0.0003363643 -0.001179409      0.003490419
75%  0.0030558833      1.066097  0.0018319185  0.011030560      0.004452554
    feature_fraction
25%       -2.1374687
50%       -1.0932481
75%       -0.5645319

1. MODEL SUMMARY:
* *********************** *
Model Summary:

R2: 0.9999921 

Average Marginal Effects:
                           Est   Std. Error     t value     Pr(>|t|)
num_leaves       -0.0006775316 1.571372e-05  -43.117190 2.978229e-24
learning_rate    -3.4958642058 1.018814e-02 -343.130816 8.275458e-46
n_estimators      0.0001547258 5.307425e-06   29.152697 3.006099e-20
max_depth         0.0000539840 3.761508e-05    1.435169 1.641438e-01
min_data_in_leaf  0.0036386780 3.869550e-06  940.336222 2.575816e-56
feature_fraction -1.3287593021 6.912165e-03 -192.234897 9.007823e-40

Quartiles of Marginal Effects:
                          25%           50%          75%
num_leaves       -0.006073830  0.0006160114  0.003055883
learning_rate    -6.370737399 -3.8038702998  1.066097189
n_estimators     -0.001346962 -0.0003363643  0.001831918
max_depth        -0.011036161 -0.0011794090  0.011030560
min_data_in_leaf  0.002516728  0.0034904192  0.004452554
feature_fraction -2.137468689 -1.0932481142 -0.564531874
$coefficients
                           Est   Std. Error     t value     Pr(>|t|)
num_leaves       -0.0006775316 1.571372e-05  -43.117190 2.978229e-24
learning_rate    -3.4958642058 1.018814e-02 -343.130816 8.275458e-46
n_estimators      0.0001547258 5.307425e-06   29.152697 3.006099e-20
max_depth         0.0000539840 3.761508e-05    1.435169 1.641438e-01
min_data_in_leaf  0.0036386780 3.869550e-06  940.336222 2.575816e-56
feature_fraction -1.3287593021 6.912165e-03 -192.234897 9.007823e-40

$qcoefficients
                          25%           50%          75%
num_leaves       -0.006073830  0.0006160114  0.003055883
learning_rate    -6.370737399 -3.8038702998  1.066097189
n_estimators     -0.001346962 -0.0003363643  0.001831918
max_depth        -0.011036161 -0.0011794090  0.011030560
min_data_in_leaf  0.002516728  0.0034904192  0.004452554
feature_fraction -2.137468689 -1.0932481142 -0.564531874

attr(,"class")
[1] "summary.krls"

2. OPTIMAL HYPERPARAMETERS:
   Lambda (regularization): 0.0006817663 
   Sigma (kernel bandwidth): 6 

3. MODEL FIT STATISTICS:
$K
            1           2          3          4           5          6
1  1.00000000 0.346289988 0.08604608 0.46583410 0.531980254 0.23136523
2  0.34628999 1.000000000 0.07352161 0.31609701 0.050345647 0.05942486
3  0.08604608 0.073521612 1.00000000 0.07500076 0.069672906 0.19728663
4  0.46583410 0.316097007 0.07500076 1.00000000 0.158483840 0.19829352
5  0.53198025 0.050345647 0.06967291 0.15848384 1.000000000 0.18004778
6  0.23136523 0.059424863 0.19728663 0.19829352 0.180047779 1.00000000
7  0.08353374 0.022254261 0.25312920 0.05563248 0.203463068 0.16867710
8  0.20166404 0.038388360 0.28570968 0.18245112 0.208883011 0.72737054
9  0.27928707 0.794316964 0.16778783 0.28598463 0.042688968 0.13623105
10 0.08435643 0.025334866 0.07646097 0.09968598 0.118803179 0.29117772
11 0.07571185 0.019969536 0.45340554 0.08249890 0.130906958 0.45668559
12 0.30303663 0.178541700 0.02973416 0.52779470 0.121535116 0.20788662
13 0.03534573 0.091144171 0.10269303 0.05488055 0.008439491 0.15630714
14 0.17088805 0.083772785 0.31665779 0.07614689 0.187044632 0.14640795
15 0.46222950 0.537663280 0.31939037 0.24602887 0.149605216 0.19522609
16 0.03635723 0.026874537 0.27745263 0.13590608 0.024263959 0.23786775
17 0.36093089 0.045295447 0.08333074 0.11940040 0.543990304 0.43042775
18 0.20236433 0.226249336 0.64783512 0.17753861 0.079026686 0.39713806
19 0.06312870 0.089130403 0.20781601 0.16601762 0.019673584 0.28888793
20 0.04716451 0.040292828 0.04475880 0.04878997 0.034647311 0.13885161
21 0.23891870 0.051138500 0.05353973 0.24701147 0.207535089 0.51824176
22 0.05135419 0.042290763 0.04223913 0.04349449 0.037121045 0.13527760
23 0.30602606 0.107732374 0.06084093 0.20287629 0.188884536 0.38222406
24 0.18617699 0.248696037 0.02466316 0.65795994 0.036487174 0.09993542
25 0.16981623 0.040955724 0.20057580 0.13782465 0.159003263 0.66063043
26 0.19139045 0.048929561 0.19088522 0.20068332 0.158632956 0.96181365
27 0.02869303 0.004393955 0.11758836 0.02596390 0.074651486 0.28853914
28 0.14412534 0.049949326 0.47996622 0.08149825 0.151951286 0.41913815
29 0.22740404 0.338765962 0.10219614 0.14327313 0.102542010 0.08291039
30 0.05680967 0.098014357 0.24221300 0.19849453 0.029190144 0.11123236
            7          8          9         10         11         12
1  0.08353374 0.20166404 0.27928707 0.08435643 0.07571185 0.30303663
2  0.02225426 0.03838836 0.79431696 0.02533487 0.01996954 0.17854170
3  0.25312920 0.28570968 0.16778783 0.07646097 0.45340554 0.02973416
4  0.05563248 0.18245112 0.28598463 0.09968598 0.08249890 0.52779470
5  0.20346307 0.20888301 0.04268897 0.11880318 0.13090696 0.12153512
6  0.16867710 0.72737054 0.13623105 0.29117772 0.45668559 0.20788662
7  1.00000000 0.16775249 0.03243262 0.49742661 0.56402602 0.06322869
8  0.16775249 1.00000000 0.08491953 0.16884237 0.49360692 0.08525776
9  0.03243262 0.08491953 1.00000000 0.03722578 0.05015200 0.17659894
10 0.49742661 0.16884237 0.03722578 1.00000000 0.37379621 0.19447656
11 0.56402602 0.49360692 0.05015200 0.37379621 1.00000000 0.07280995
12 0.06322869 0.08525776 0.17659894 0.19447656 0.07280995 1.00000000
13 0.05635948 0.08648542 0.18849557 0.14706525 0.09126903 0.04824994
14 0.38980010 0.21497344 0.09812921 0.18574599 0.23419492 0.03108749
15 0.08779619 0.20655751 0.62443052 0.05686089 0.10213028 0.09429782
16 0.13554587 0.35174223 0.06469527 0.16595863 0.39418690 0.04950084
17 0.23082770 0.25192233 0.06376506 0.23377337 0.23824100 0.23127387
18 0.12322873 0.36437899 0.49923265 0.08264504 0.30276374 0.09691570
19 0.07414916 0.28703283 0.19320140 0.15123801 0.20180365 0.07260919
20 0.24769163 0.05021887 0.05660321 0.64688483 0.14034912 0.13782273
21 0.17118178 0.37506951 0.06717402 0.52467110 0.21583879 0.26764920
22 0.23070362 0.05051843 0.05711408 0.59495921 0.12234715 0.11406771
23 0.09568708 0.13928907 0.16140138 0.17161395 0.13812536 0.54436559
24 0.01742562 0.05078508 0.24577592 0.05506153 0.03090827 0.67176038
25 0.14039623 0.42253863 0.10441903 0.14859715 0.41712771 0.19942358
26 0.17727198 0.66406842 0.11771286 0.31026727 0.50699701 0.23917213
27 0.46795417 0.28657319 0.01045290 0.54187859 0.58349973 0.02998785
28 0.29679549 0.60679795 0.10174221 0.18681680 0.47411792 0.03407665
29 0.16950689 0.03473544 0.30883491 0.14858424 0.07671845 0.26502233
30 0.19254232 0.08082403 0.16064136 0.17719862 0.25246086 0.19203908
            13         14         15         16         17         18
1  0.035345734 0.17088805 0.46222950 0.03635723 0.36093089 0.20236433
2  0.091144171 0.08377278 0.53766328 0.02687454 0.04529545 0.22624934
3  0.102693034 0.31665779 0.31939037 0.27745263 0.08333074 0.64783512
4  0.054880549 0.07614689 0.24602887 0.13590608 0.11940040 0.17753861
5  0.008439491 0.18704463 0.14960522 0.02426396 0.54399030 0.07902669
6  0.156307139 0.14640795 0.19522609 0.23786775 0.43042775 0.39713806
7  0.056359482 0.38980010 0.08779619 0.13554587 0.23082770 0.12322873
8  0.086485422 0.21497344 0.20655751 0.35174223 0.25192233 0.36437899
9  0.188495574 0.09812921 0.62443052 0.06469527 0.06376506 0.49923265
10 0.147065247 0.18574599 0.05686089 0.16595863 0.23377337 0.08264504
11 0.091269028 0.23419492 0.10213028 0.39418690 0.23824100 0.30276374
12 0.048249942 0.03108749 0.09429782 0.04950084 0.23127387 0.09691570
13 1.000000000 0.14261633 0.16114542 0.19014564 0.02311174 0.21669952
14 0.142616329 1.00000000 0.37709671 0.13932554 0.10706054 0.21599740
15 0.161145421 0.37709671 1.00000000 0.09157961 0.11781746 0.56481637
16 0.190145638 0.13932554 0.09157961 1.00000000 0.03059614 0.23418518
17 0.023111738 0.10706054 0.11781746 0.03059614 1.00000000 0.14260731
18 0.216699516 0.21599740 0.56481637 0.23418518 0.14260731 1.00000000
19 0.587162420 0.16898499 0.20619648 0.63542191 0.03202974 0.34113046
20 0.291688463 0.13165649 0.05582112 0.07003192 0.10285788 0.06736485
21 0.147526218 0.17658582 0.11805697 0.16862292 0.28140072 0.10860162
22 0.313634914 0.15791032 0.06431247 0.06029259 0.10114683 0.06575047
23 0.039792623 0.03856414 0.11499272 0.03053815 0.60808968 0.18312776
24 0.039383590 0.01400863 0.08932779 0.05613455 0.05614994 0.09362618
25 0.042489698 0.05597141 0.11297738 0.11023937 0.49934246 0.35780744
26 0.129063909 0.10964327 0.14682185 0.25265479 0.42658081 0.36536614
27 0.086897612 0.20532893 0.03225830 0.22614095 0.13705479 0.07506563
28 0.191193255 0.62363820 0.33592165 0.30667217 0.15548200 0.41802795
29 0.082605104 0.12697780 0.23542668 0.02462642 0.17080283 0.17082390
30 0.104032235 0.07292830 0.09605307 0.27262535 0.05345054 0.22879608
           19         20         21         22         23         24         25
1  0.06312870 0.04716451 0.23891870 0.05135419 0.30602606 0.18617699 0.16981623
2  0.08913040 0.04029283 0.05113850 0.04229076 0.10773237 0.24869604 0.04095572
3  0.20781601 0.04475880 0.05353973 0.04223913 0.06084093 0.02466316 0.20057580
4  0.16601762 0.04878997 0.24701147 0.04349449 0.20287629 0.65795994 0.13782465
5  0.01967358 0.03464731 0.20753509 0.03712105 0.18888454 0.03648717 0.15900326
6  0.28888793 0.13885161 0.51824176 0.13527760 0.38222406 0.09993542 0.66063043
7  0.07414916 0.24769163 0.17118178 0.23070362 0.09568708 0.01742562 0.14039623
8  0.28703283 0.05021887 0.37506951 0.05051843 0.13928907 0.05078508 0.42253863
9  0.19320140 0.05660321 0.06717402 0.05711408 0.16140138 0.24577592 0.10441903
10 0.15123801 0.64688483 0.52467110 0.59495921 0.17161395 0.05506153 0.14859715
11 0.20180365 0.14034912 0.21583879 0.12234715 0.13812536 0.03090827 0.41712771
12 0.07260919 0.13782273 0.26764920 0.11406771 0.54436559 0.67176038 0.19942358
13 0.58716242 0.29168846 0.14752622 0.31363491 0.03979262 0.03938359 0.04248970
14 0.16898499 0.13165649 0.17658582 0.15791032 0.03856414 0.01400863 0.05597141
15 0.20619648 0.05582112 0.11805697 0.06431247 0.11499272 0.08932779 0.11297738
16 0.63542191 0.07003192 0.16862292 0.06029259 0.03053815 0.05613455 0.11023937
17 0.03202974 0.10285788 0.28140072 0.10114683 0.60808968 0.05614994 0.49934246
18 0.34113046 0.06736485 0.10860162 0.06575047 0.18312776 0.09362618 0.35780744
19 1.00000000 0.12811529 0.23250392 0.12607833 0.04561090 0.08729144 0.09233471
20 0.12811529 1.00000000 0.26289261 0.97262680 0.12103637 0.04080366 0.06042012
21 0.23250392 0.26289261 1.00000000 0.27374045 0.20250670 0.10576336 0.17727481
22 0.12607833 0.97262680 0.27374045 1.00000000 0.10587179 0.03199563 0.05123700
23 0.04561090 0.12103637 0.20250670 0.10587179 1.00000000 0.22003748 0.54950698
24 0.08729144 0.04080366 0.10576336 0.03199563 0.22003748 1.00000000 0.09473493
25 0.09233471 0.06042012 0.17727481 0.05123700 0.54950698 0.09473493 1.00000000
26 0.25965784 0.13780613 0.46501186 0.12586172 0.42382255 0.11704748 0.75342141
27 0.13457913 0.21405456 0.30415123 0.20820922 0.04969150 0.00731568 0.13042827
28 0.32979054 0.09678693 0.25197916 0.10979976 0.06484106 0.01711810 0.18219854
29 0.04708646 0.23722230 0.07608147 0.22281049 0.28327161 0.13463036 0.09406100
30 0.18607513 0.13634296 0.06897490 0.09912534 0.11535266 0.20396861 0.13817054
           26          27         28         29         30
1  0.19139045 0.028693033 0.14412534 0.22740404 0.05680967
2  0.04892956 0.004393955 0.04994933 0.33876596 0.09801436
3  0.19088522 0.117588358 0.47996622 0.10219614 0.24221300
4  0.20068332 0.025963899 0.08149825 0.14327313 0.19849453
5  0.15863296 0.074651486 0.15195129 0.10254201 0.02919014
6  0.96181365 0.288539142 0.41913815 0.08291039 0.11123236
7  0.17727198 0.467954170 0.29679549 0.16950689 0.19254232
8  0.66406842 0.286573190 0.60679795 0.03473544 0.08082403
9  0.11771286 0.010452896 0.10174221 0.30883491 0.16064136
10 0.31026727 0.541878589 0.18681680 0.14858424 0.17719862
11 0.50699701 0.583499728 0.47411792 0.07671845 0.25246086
12 0.23917213 0.029987846 0.03407665 0.26502233 0.19203908
13 0.12906391 0.086897612 0.19119325 0.08260510 0.10403223
14 0.10964327 0.205328927 0.62363820 0.12697780 0.07292830
15 0.14682185 0.032258304 0.33592165 0.23542668 0.09605307
16 0.25265479 0.226140952 0.30667217 0.02462642 0.27262535
17 0.42658081 0.137054791 0.15548200 0.17080283 0.05345054
18 0.36536614 0.075065626 0.41802795 0.17082390 0.22879608
19 0.25965784 0.134579132 0.32979054 0.04708646 0.18607513
20 0.13780613 0.214054560 0.09678693 0.23722230 0.13634296
21 0.46501186 0.304151229 0.25197916 0.07608147 0.06897490
22 0.12586172 0.208209224 0.10979976 0.22281049 0.09912534
23 0.42382255 0.049691497 0.06484106 0.28327161 0.11535266
24 0.11704748 0.007315680 0.01711810 0.13463036 0.20396861
25 0.75342141 0.130428273 0.18219854 0.09406100 0.13817054
26 1.00000000 0.289716118 0.33379602 0.08311499 0.14584314
27 0.28971612 1.000000000 0.36039034 0.02655176 0.06592102
28 0.33379602 0.360390335 1.00000000 0.05985102 0.07721934
29 0.08311499 0.026551763 0.05985102 1.00000000 0.23185448
30 0.14584314 0.065921022 0.07721934 0.23185448 1.00000000

$coeffs
             [,1]
 [1,]  -0.7138638
 [2,]   1.7899866
 [3,]   0.1927768
 [4,]  -0.5532582
 [5,]   0.1941038
 [6,]  -1.4142678
 [7,]  -2.6543658
 [8,]   1.7508142
 [9,]  -1.1009789
[10,]   2.3333399
[11,]   1.3515547
[12,]   2.2094337
[13,]  -2.0909906
[14,]  -0.4938505
[15,]   0.4587227
[16,]  -1.5901434
[17,]   0.7368818
[18,]  -0.3543444
[19,]   3.0886970
[20,]  13.9493343
[21,]   0.0591846
[22,] -15.0397146
[23,]   1.4393512
[24,]  -0.3981617
[25,]   2.3468539
[26,]  -2.8810285
[27,]   0.2784308
[28,]  -0.2658538
[29,]  -2.1023006
[30,]  -1.6524928

$Looe
         [,1]
[1,] 3.114752

$fitted
          [,1]
1  -0.47313641
2  -0.46018724
3  -0.63429308
4  -0.43524898
5  -0.43773490
6  -0.47123303
7  -0.87920805
8  -0.37722021
9  -0.60194892
10 -0.22914917
11 -0.45430777
12  0.02800671
13 -0.95094846
14 -0.93542454
15 -0.61891497
16 -0.54133782
17 -0.13049601
18 -0.62118064
19 -0.44020187
20 -0.66370969
21 -0.42781842
22 -0.91261541
23  0.08051529
24 -0.32659728
25 -0.10211872
26 -0.38212339
27 -0.43658341
28 -0.62576642
29 -0.93854201
30 -0.86613036

$X
      num_leaves learning_rate n_estimators max_depth min_data_in_leaf
 [1,]         45    0.07067682          100        10              100
 [2,]         45    0.09551503           50        10               50
 [3,]         45    0.05648004          150        -1               20
 [4,]         31    0.06188671          100        10              100
 [5,]         45    0.04026981          150        10              100
 [6,]         31    0.04125922          100        -1              100
 [7,]         31    0.01180219          150         5               20
 [8,]         31    0.05525317          150        -1              100
 [9,]         45    0.08839391           50         5               50
[10,]         15    0.01056707          100         5               50
[11,]         31    0.01648514          150        -1               50
[12,]         31    0.02477901           50        10              100
[13,]         15    0.07933007           50        -1               20
[14,]         31    0.07616659          150         5               20
[15,]         45    0.09746881          100         5               50
[16,]         15    0.05198251          150        -1               50
[17,]         45    0.01669461          100         5              100
[18,]         45    0.06839363          100        -1               50
[19,]         15    0.07827339          100        -1               50
[20,]         15    0.02233955           50         5               20
[21,]         15    0.04569261          100         5              100
[22,]         15    0.03024868           50         5               20
[23,]         45    0.01521627           50         5              100
[24,]         31    0.04563034           50        10              100
[25,]         45    0.01584355          100        -1              100
[26,]         31    0.03032978          100        -1              100
[27,]         15    0.01491662          150        -1               50
[28,]         31    0.07032538          150        -1               50
[29,]         45    0.03679676           50        10               20
[30,]         31    0.01906494          100         5               20
      feature_fraction
 [1,]        0.8246258
 [2,]        0.7622057
 [3,]        0.7784393
 [4,]        0.7404175
 [5,]        0.8705561
 [6,]        0.8213660
 [7,]        0.8512196
 [8,]        0.8125034
 [9,]        0.7551798
[10,]        0.8471117
[11,]        0.8098560
[12,]        0.7692254
[13,]        0.8029931
[14,]        0.8631536
[15,]        0.8052545
[16,]        0.7406080
[17,]        0.8696215
[18,]        0.7740988
[19,]        0.7606650
[20,]        0.8541194
[21,]        0.8466897
[22,]        0.8677812
[23,]        0.8138098
[24,]        0.7052562
[25,]        0.7972254
[26,]        0.8085362
[27,]        0.8673320
[28,]        0.8457329
[29,]        0.8110228
[30,]        0.7146829

$y
             [,1]
 [1,] -0.47327065
 [2,] -0.45985065
 [3,] -0.63425683
 [4,] -0.43535302
 [5,] -0.43769840
 [6,] -0.47149897
 [7,] -0.87970718
 [8,] -0.37689099
 [9,] -0.60215595
[10,] -0.22871041
[11,] -0.45405362
[12,]  0.02842218
[13,] -0.95134165
[14,] -0.93551740
[15,] -0.61882871
[16,] -0.54163683
[17,] -0.13035745
[18,] -0.62124727
[19,] -0.43962106
[20,] -0.66108664
[21,] -0.42780729
[22,] -0.91544349
[23,]  0.08078594
[24,] -0.32667215
[25,] -0.10167741
[26,] -0.38266514
[27,] -0.43653105
[28,] -0.62581641
[29,] -0.93893733
[30,] -0.86644109

$sigma
[1] 6

$lambda
             [,1]
[1,] 0.0006817663

$R2
          [,1]
[1,] 0.9999921

$derivatives
         num_leaves learning_rate  n_estimators     max_depth min_data_in_leaf
 [1,]  1.466634e-03   -3.91848727 -0.0014837374 -0.0048548837     0.0033288224
 [2,]  1.952469e-03    4.78968673 -0.0007401287  0.0206455422     0.0030324067
 [3,]  5.819306e-03    1.08513623  0.0022512588 -0.0330900165     0.0035415503
 [4,] -1.009628e-03   -3.21963314 -0.0029543239  0.0006901616     0.0020033751
 [5,]  1.873337e-03   -3.64769308 -0.0013601104 -0.0145351414     0.0041366143
 [6,]  9.379902e-03   -6.37372085  0.0020946537  0.0262232220     0.0013726113
 [7,] -9.289843e-03   -6.70108654 -0.0009177923 -0.0223401580     0.0066131584
 [8,]  4.738914e-03   -1.41260681  0.0024092752 -0.0004274860     0.0010590804
 [9,]  3.056838e-03    4.24885061 -0.0002210989  0.0209612193     0.0039592013
[10,] -1.114425e-02  -12.21406207 -0.0025210637  0.0061015727     0.0058590933
[11,]  5.481047e-04   -3.97942649 -0.0004914069 -0.0215230723     0.0060987822
[12,] -1.961513e-04   -6.41720401 -0.0012996865 -0.0100783752     0.0027662047
[13,] -8.114291e-03    1.37902296  0.0028241154 -0.0199188869     0.0031928470
[14,]  1.363518e-03    6.03273331  0.0042100759 -0.0094267820     0.0030486752
[15,]  5.222021e-03    5.55833895  0.0010437128  0.0047934290     0.0034254911
[16,] -4.198528e-03    3.32916677 -0.0013075171 -0.0113554226     0.0024335689
[17,]  3.053019e-03   -5.97011913 -0.0021140404 -0.0019313320     0.0042235195
[18,]  4.964972e-03    0.07300528  0.0025377603 -0.0168740276     0.0045288982
[19,] -8.020141e-03    3.26985802  0.0022986583 -0.0074561140     0.0034392881
[20,] -1.266259e-02  -20.01947459  0.0007305896  0.0091392721     0.0058191864
[21,] -1.849531e-03   -7.70650178  0.0007906704  0.0215267317     0.0019649822
[22,] -1.224125e-02  -19.09425196  0.0007103946  0.0101466014     0.0051524511
[23,] -2.943899e-03   -6.36178706  0.0009000596  0.0124694123     0.0039581927
[24,] -9.088437e-05   -4.02948495 -0.0019004744  0.0039816771     0.0021494519
[25,]  9.896435e-03   -5.56200513 -0.0004516296  0.0313928086     0.0016025581
[26,]  1.081062e-02   -7.15146536  0.0010260161  0.0342898434     0.0005407147
[27,] -6.698931e-03   -5.06452614 -0.0006020958 -0.0042421068     0.0035933148
[28,]  6.839180e-04    1.00898006  0.0035186938 -0.0279919453     0.0052017509
[29,]  1.026719e-03   -3.68925333 -0.0023793391  0.0113252134     0.0071126569
[30,] -7.722759e-03   -3.11791542 -0.0019597167 -0.0060214366     0.0040018918
      feature_fraction
 [1,]     -1.130705914
 [2,]     -1.333755975
 [3,]     -0.560086679
 [4,]      1.639316837
 [5,]     -0.761448884
 [6,]     -1.436435039
 [7,]     -1.055790315
 [8,]     -0.577867459
 [9,]     -1.343874436
[10,]     -4.146393405
[11,]     -0.004762551
[12,]      2.330924021
[13,]     -5.514804447
[14,]     -0.971536878
[15,]     -1.924830440
[16,]      1.670745806
[17,]     -3.560164436
[18,]     -0.798497972
[19,]     -2.287127860
[20,]     -6.861491470
[21,]     -2.852144134
[22,]     -6.420371092
[23,]     -1.049280231
[24,]      3.796480779
[25,]      0.611629791
[26,]     -0.678785223
[27,]     -1.817482076
[28,]     -2.208348106
[29,]     -1.688102670
[30,]      1.072211395

$avgderivatives
        num_leaves learning_rate n_estimators  max_depth min_data_in_leaf
[1,] -0.0006775316     -3.495864 0.0001547258 5.3984e-05      0.003638678
     feature_fraction
[1,]        -1.328759

$var.avgderivatives
       num_leaves learning_rate n_estimators    max_depth min_data_in_leaf
[1,] 2.469211e-10  0.0001037982 2.816876e-11 1.414894e-09     1.497342e-11
     feature_fraction
[1,]     4.777802e-05

$vcov.c
               [,1]          [,2]          [,3]          [,4]          [,5]
 [1,]  7.198390e-06 -2.176901e-06 -2.707928e-07 -3.939010e-06 -4.491910e-06
 [2,] -2.176901e-06  1.450342e-05 -4.479936e-06 -5.349111e-07  1.007133e-06
 [3,] -2.707928e-07 -4.479936e-06  7.331466e-06  5.334838e-07  5.249473e-07
 [4,] -3.939010e-06 -5.349111e-07  5.334838e-07  5.675790e-06  1.925799e-06
 [5,] -4.491910e-06  1.007133e-06  5.249473e-07  1.925799e-06  5.276935e-06
 ...

$vcov.fitted
               1             2             3             4             5
1   5.770597e-07  3.586715e-10 -4.683216e-11  7.280141e-10  8.245260e-10
2   3.586715e-10  5.761571e-07  3.452175e-10  1.418792e-10 -1.615939e-10
3  -4.683216e-11  3.452175e-10  5.769929e-07 -2.115664e-11 -1.518574e-11
4   7.280141e-10  1.418792e-10 -2.115664e-11  5.770635e-07 -1.658241e-10
5   8.245260e-10 -1.615939e-10 -1.518574e-11 -1.658241e-10  5.773684e-07
...

$binaryindicator
     num_leaves learning_rate n_estimators max_depth min_data_in_leaf
[1,]      FALSE         FALSE        FALSE     FALSE            FALSE
     feature_fraction
[1,]            FALSE

attr(,"class")
[1] "krls"

4. PARTIAL DERIVATIVES (Average Marginal Effects):
      num_leaves    learning_rate     n_estimators        max_depth 
   -0.0006775316    -3.4958642058     0.0001547258     0.0000539840 
min_data_in_leaf feature_fraction 
    0.0036386780    -1.3287593021 

6. GENERATING DIAGNOSTIC PLOTS...
   Diagnostic plots saved to 'krls_diagnostics_r.png'

7. GAP ANALYSIS BY HYPERPARAMETER:


`geom_smooth()` using formula = 'y ~ x'

image-title-here

`geom_smooth()` using formula = 'y ~ x'
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“pseudoinverse used at 14.85”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“neighborhood radius 30.15”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“reciprocal condition number  4.5167e-17”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“There are other near singularities as well. 200.22”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“pseudoinverse used at 14.85”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“neighborhood radius 30.15”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“reciprocal condition number  4.5167e-17”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“There are other near singularities as well. 200.22”

image-title-here

image-title-here

`geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“pseudoinverse used at 14.85”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“neighborhood radius 30.15”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“reciprocal condition number  4.5167e-17”
Warning message in simpleLoess(y, x, w, span, degree = degree, parametric = parametric, :
“There are other near singularities as well. 200.22”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“pseudoinverse used at 14.85”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“neighborhood radius 30.15”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“reciprocal condition number  4.5167e-17”
Warning message in predLoess(object$y, object$x, newx = if (is.null(newdata)) object$x else if (is.data.frame(newdata)) as.matrix(model.frame(delete.response(terms(object)), :
“There are other near singularities as well. 200.22”


   Gap analysis plots saved to 'gap_analysis_plots_r.png'

8. BEST HYPERPARAMETER CONFIGURATIONS:

Top 3 configurations with smallest gap (best generalization):

Rank 1 :
  Gap: 0.02842218 
  CV RMSE: 6.70449 
  Test RMSE: 6.676068 
  num_leaves: 31 
  learning_rate: 0.02477901 
  n_estimators: 50 
  max_depth: 10 
  min_data_in_leaf: 100 
  feature_fraction: 0.7692254 

Rank 2 :
  Gap: 0.08078594 
  CV RMSE: 7.269937 
  Test RMSE: 7.189151 
  num_leaves: 45 
  learning_rate: 0.01521627 
  n_estimators: 50 
  max_depth: 5 
  min_data_in_leaf: 100 
  feature_fraction: 0.8138098 

Rank 3 :
  Gap: -0.1016774 
  CV RMSE: 6.372935 
  Test RMSE: 6.474612 
  num_leaves: 45 
  learning_rate: 0.01584355 
  n_estimators: 100 
  max_depth: -1 
  min_data_in_leaf: 100 
  feature_fraction: 0.7972254 


Top 3 configurations with largest gap (most overfitting):

Rank 1 :
  Gap: -0.9513416 
  CV RMSE: 3.585176 
  Test RMSE: 4.536517 
  num_leaves: 15 
  learning_rate: 0.07933007 
  n_estimators: 50 
  max_depth: -1 
  min_data_in_leaf: 20 
  feature_fraction: 0.8029931 

Rank 2 :
  Gap: -0.9389373 
  CV RMSE: 3.989341 
  Test RMSE: 4.928279 
  num_leaves: 45 
  learning_rate: 0.03679676 
  n_estimators: 50 
  max_depth: 10 
  min_data_in_leaf: 20 
  feature_fraction: 0.8110228 

Rank 3 :
  Gap: -0.9355174 
  CV RMSE: 3.232667 
  Test RMSE: 4.168185 
  num_leaves: 31 
  learning_rate: 0.07616659 
  n_estimators: 150 
  max_depth: 5 
  min_data_in_leaf: 20 
  feature_fraction: 0.8631536 

9. STATISTICAL ANALYSIS OF GAP:
   Mean gap: -0.5088622 
   Standard deviation: 0.2758146 
   Minimum gap: -0.9513416 
   Maximum gap: 0.08078594 
   Median gap: -0.4656748 
   t-test for gap = 0: t = -10.10517 , p-value = 5.20261e-11 
   Conclusion: Gap is significantly different from zero (p < 0.05)
overfitting?



	One Sample t-test

data:  results_table$gap
t = -10.105, df = 29, p-value = 1
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
 -0.5944245        Inf
sample estimates:
 mean of x 
-0.5088622 



underfitting?



	One Sample t-test

data:  results_table$gap
t = -10.105, df = 29, p-value = 2.601e-11
alternative hypothesis: true mean is less than 0
95 percent confidence interval:
       -Inf -0.4232999
sample estimates:
 mean of x 
-0.5088622 

✅ All R code executed successfully!

image-title-here

Comments powered by Talkyard.