In OSIC Pulmonary Fibrosis Progression competition on Kaggle, participants are tasked to determine the likelihood of recovery (prognosis) of several patients affected by a lung disease. For each patient, the maximum volume of air they can exhale after a maximum inhalation (FVC, Forced Vital Capacity) is measured over the weeks, for approximately 1-2 years of time.

In addition, we have the following information about these people:

  • A chest computer scan obtained at time Week=0
  • Their age
  • Their sex
  • Their smoking status: currently smokes, ex-smoker, never smoked

The challenge is to assess the lung function’s health by forecasting the FVC (I’m not asking myself here, if it’s the good or bad way to do that). What I like about this competition, is that there are many ways to approach it. Here’s a non-exhaustive list:

1.One way could be to construct a Statistical/Machine Learning (ML) model on the whole dataset, and study the (conditional) distribution of the FVC, knowing the scan, age, sex, and smoking status. In this first approach we consider that disease evolution can be generalized among categories of patients sharing the same patterns. A Bayesian ML model could capture the uncertainty around predictions, or we could use a more or less sophisticated bootstrapping procedure for the same purpose. Or, even, consider that ML model residuals are irregularly spaced time series.

2.Another way, the quick and dirty one I’ll present here, considers each patient’s case individually. Age, sex, smoking status and the chest scan are not used, but the measurement week is. If we are only interested in forecasting the FVC, the approach will be fine. But if we want to understand how each one of the factors we previously described influence the FVC, either individually or in conjunction, then the first approach is better.

0 - Functions

These are the functions that I use in the analysis. The first one extracts a patient’s information from the whole database, based on his/her identifier. The second one fits a smoothing spline to a patient’s data, and forecasts his/her FVC.

get patient data


suppressPackageStartupMessages(library(dplyr))

# 0 - 1 get patient data -----
get_patient_data <- function(id, train)
{
  df <- dplyr::select(dplyr::filter(train, Patient == id), c(Weeks, FVC))
  df$log_Weeks <- log(13 + df$Weeks) # the relative timing of FVC measurements (varies widely)
  df$log_FVC <- log(df$FVC) # transformed response variable
  df$Patient <- id
  return(df)
}

fit and forecast FVC

# 0 - 2 fit, predict and plot -----
fit_predict <- function(df, plot_=TRUE)
{
  min_week <- 13
  n <- nrow(df)

  test_seq_week <- seq(-12, 133)
  log_test_seq_week <- log(min_week + test_seq_week)
  
    
    # Fit a smoothing spline, using Leave-one-out cross-validation for regularization
    fit_obj <- stats::smooth.spline(x = df$log_Weeks,
                                    y = df$log_FVC,
                                    cv = TRUE)

    resids <- residuals(fit_obj)
    mean_resids <- mean(resids)
    conf <- max(exp(sd(resids)), 70) # https://www.kaggle.com/c/osic-pulmonary-fibrosis-progression/overview/evaluation

    preds <- predict(fit_obj, x=log_test_seq_week)

    res <- list(Weeks_pred = test_seq_week, FVC_pred = exp(preds$y))
    conf_sqrt_n <- conf/sqrt(n)
    ubound <- res$FVC_pred + mean_resids + 1.96*conf_sqrt_n # strong hypothesis
    lbound  <- res$FVC_pred + mean_resids - 1.96*conf_sqrt_n


  if (plot_)
  {
    leg.txt <- c("Measured FVC", "Interpolated/Extrapolated FVC", "95% Confidence interval bound")
    
    plot(df$Weeks, df$FVC, col="blue", type="l", lwd=3,
         xlim = c(-12, 133), 
         ylim = c(min(min(lbound), min(df$FVC)),
                  max(max(ubound), max(df$FVC)) ),
         xlab = "Week", ylab = "FVC",
         main = paste0("Patient: ", df$Patient[1]))
    lines(res$Weeks_pred, res$FVC_pred)
    lines(res$Weeks_pred, ubound, lty=2, col="red")
    lines(res$Weeks_pred, lbound, lty=2, col="red")
    abline(v = max(df$Weeks), lty=2)
    legend("bottomright", legend = leg.txt, 
           lwd=c(3, 1, 1), lty=c(1, 1, 2), 
           col = c("blue", "black", "red"))
  }

  return(invisible(list(res = res,
              conf = rep(conf, length(res$FVC_pred)),
              mean = res$FVC_pred,
              ubound = ubound,
              lbound = lbound,
              resids = resids)))
}

1 - Import the whole dataset

# Training set data
train <- read.csv("~/Documents/Kaggle/OSIC_August2020/train.csv")

# Training set snippet
print(head(train))
print(tail(train))

new-techtonique-website

2 - Predict FVC for a few patients (4)

# Four patient ids are selected
ids <- c("ID00421637202311550012437", "ID00422637202311677017371",
         "ID00426637202313170790466", "ID00248637202266698862378")

#par(mfrow=c(2, 2))
for(i in 1:length(ids))
{
  # Extract patient's data based on his/her ID
  (df <- get_patient_data(id=ids[i], train))
  # Obtain FVC forecasts, with 95% confidence interval
  # warnings when repeated measures in the same week
  suppressWarnings(fit_predict(df, plot_=TRUE))
}

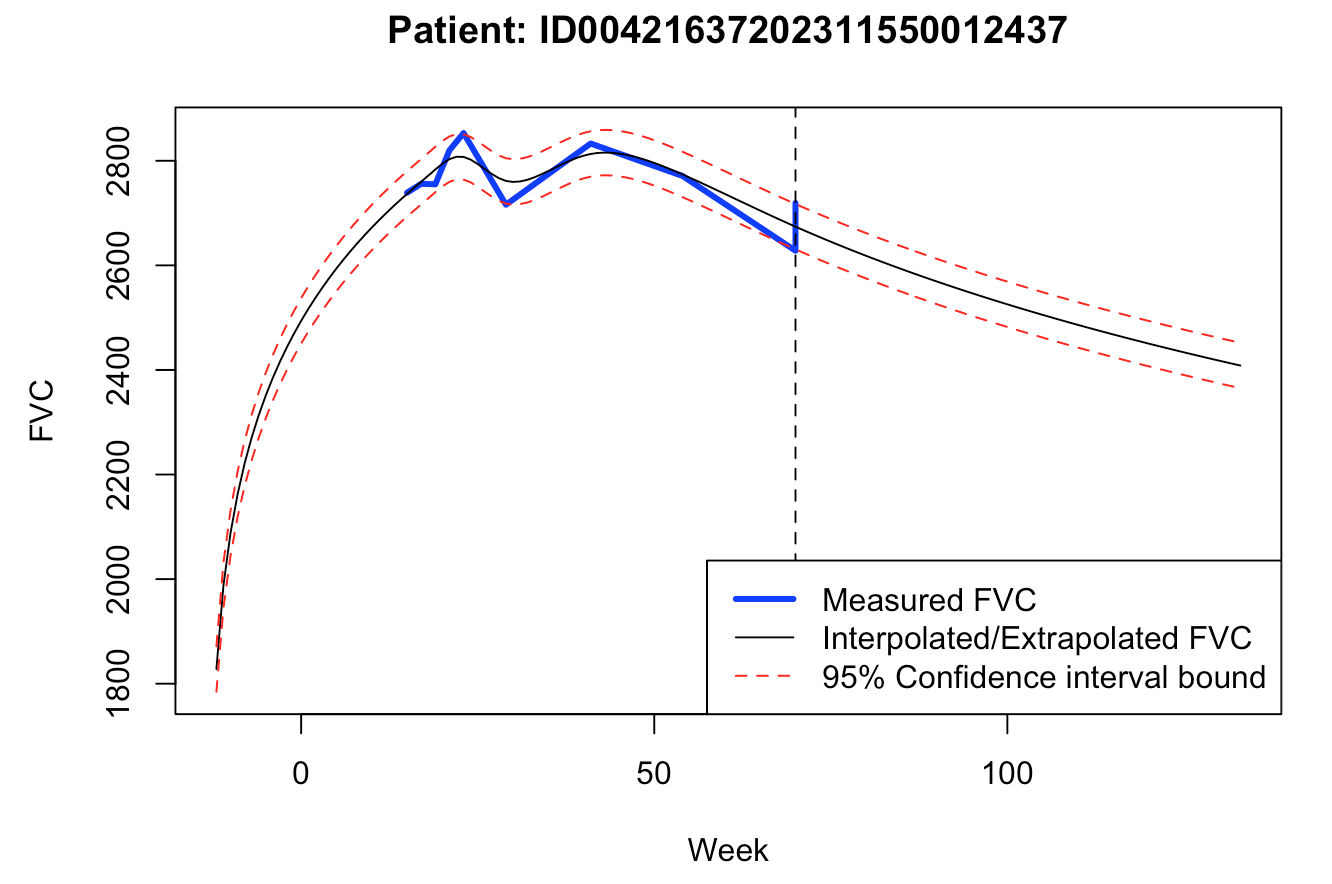
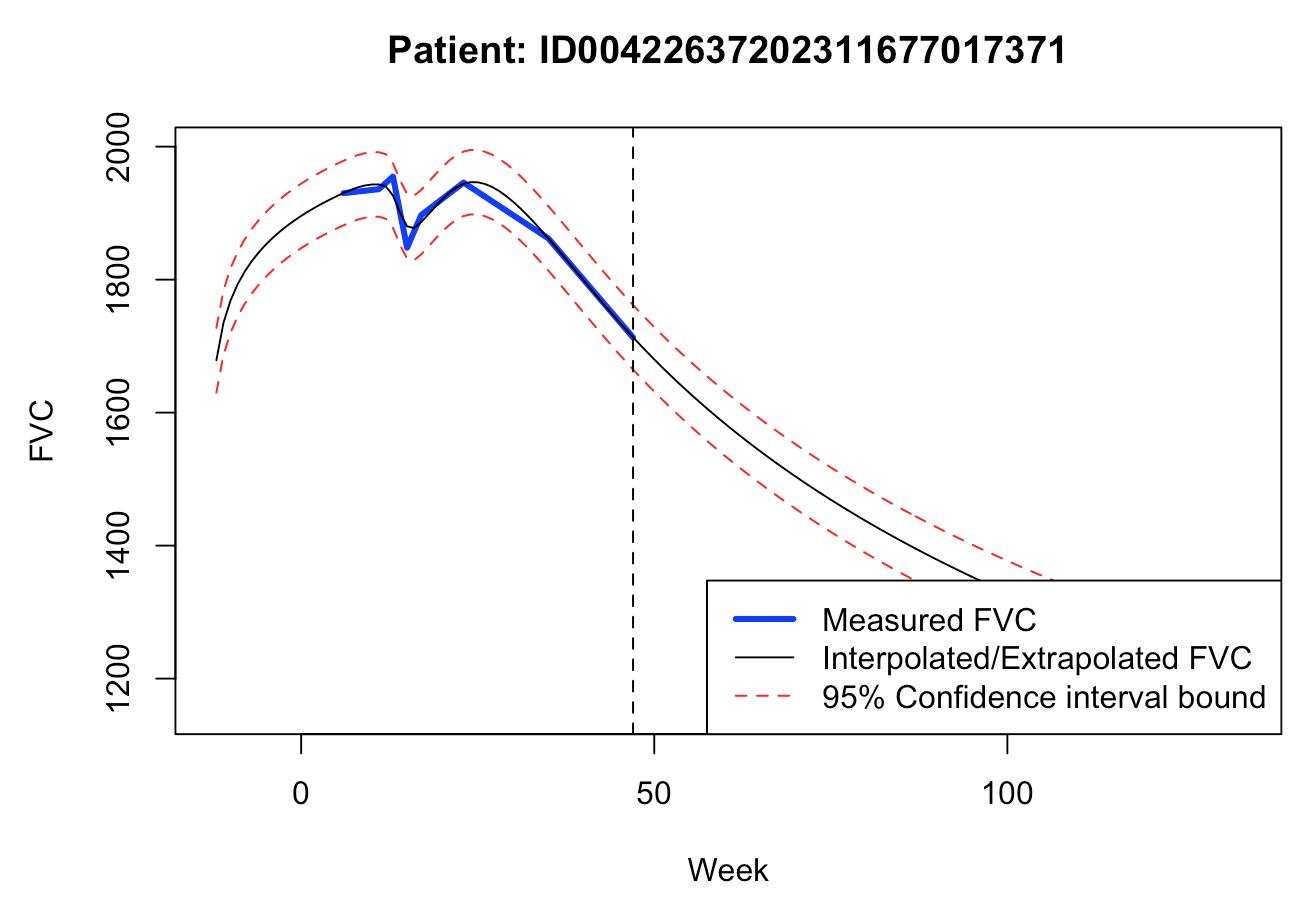
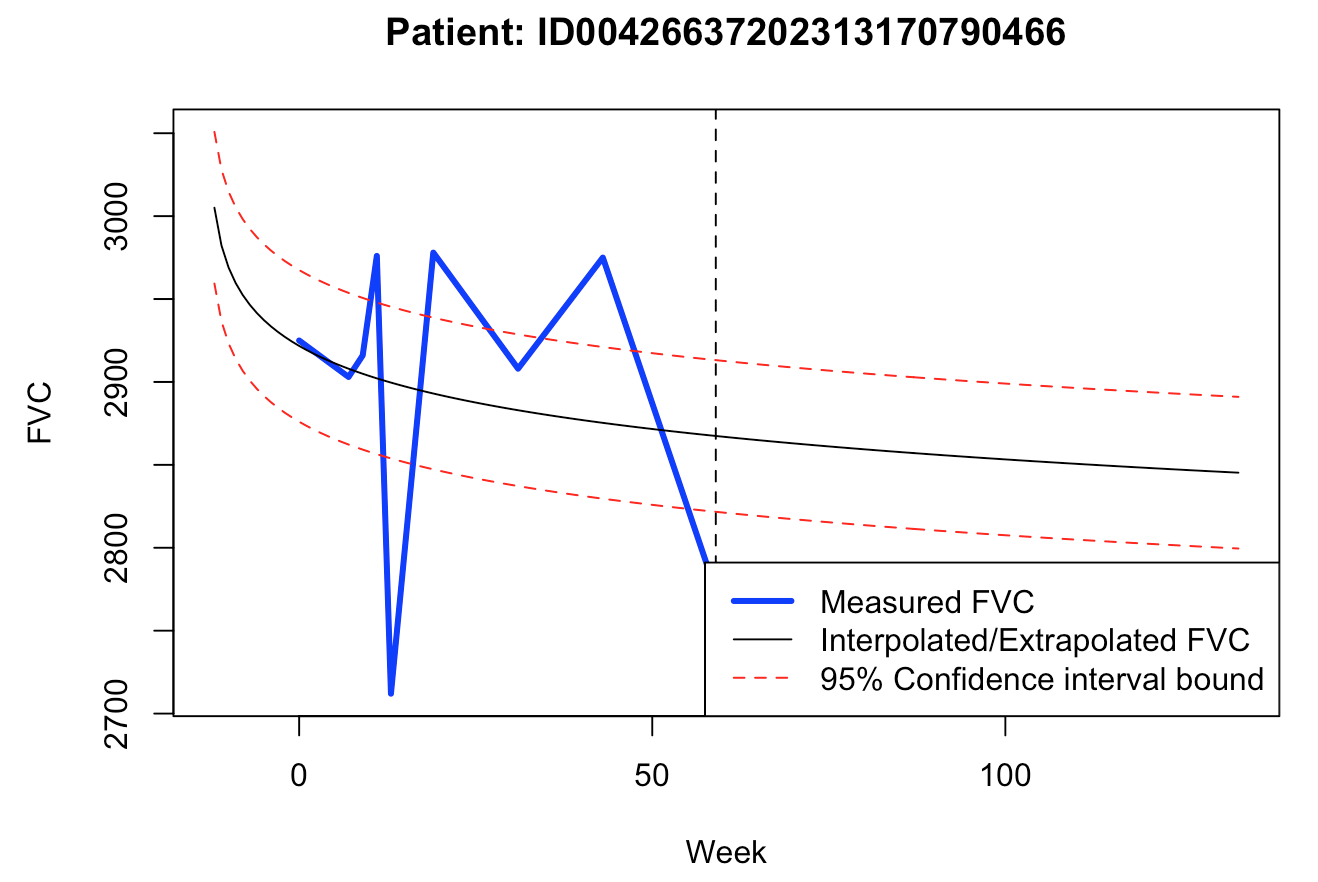
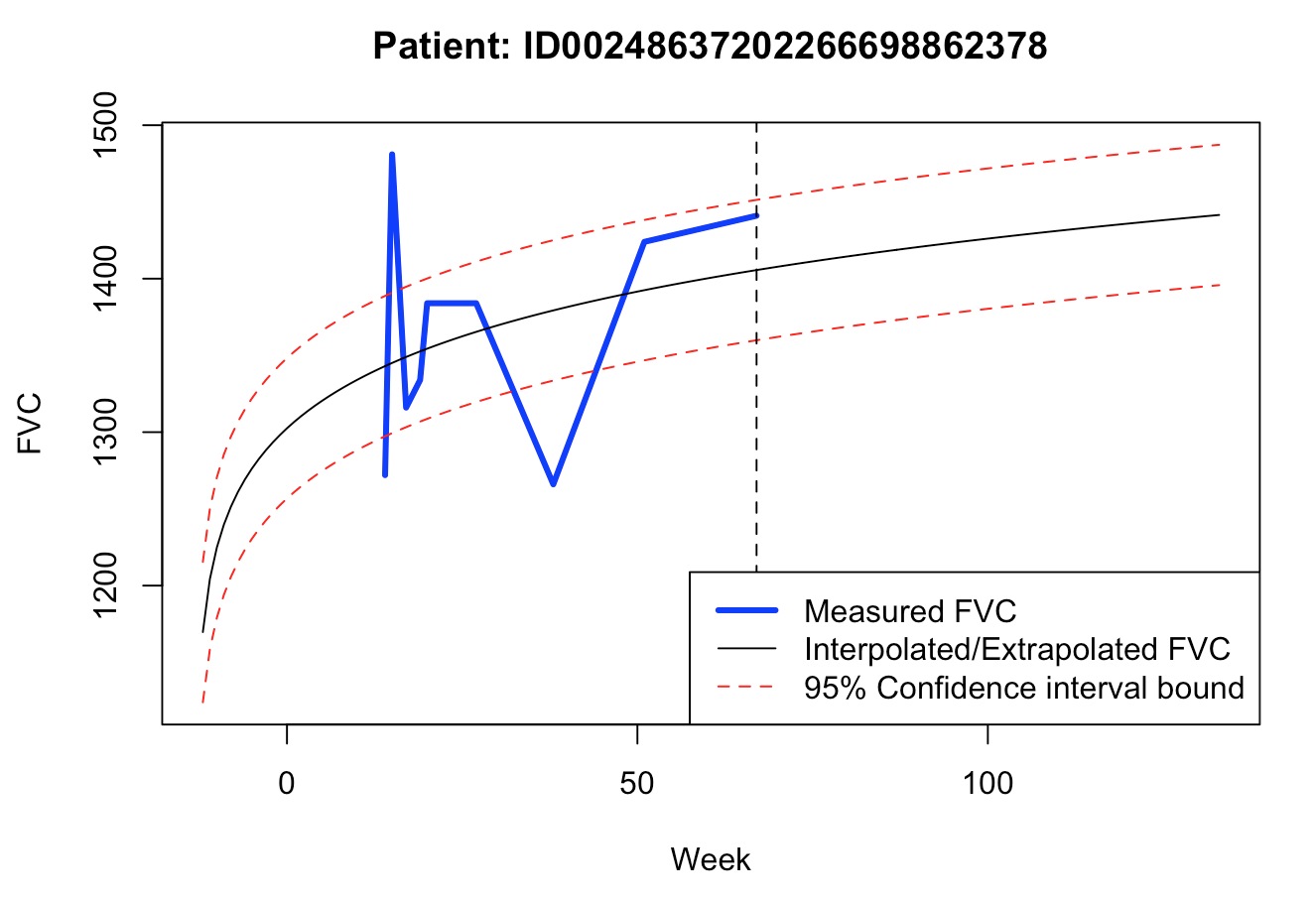
new-techtonique-website

new-techtonique-website

new-techtonique-website

new-techtonique-website

For a quick and dirty baseline model, this one seems to produce quite coherent forecasts, which could be used for decision making. Of course, validation data (unseen by the model) could reveal a whole different truth.

Comments powered by Talkyard.