There is a plethora of Automated Machine Learning tools in the wild, implementing Machine Learning (ML) pipelines from data cleaning to model validation. In this post, the input data set is already cleaned and pre-processed (diabetes dataset); the ML model is already chosen too, mlsauce’s LSBoost. We are going to focus on two important steps of a ML pipeline:

  • LSBoost’s hyperparameter tuning with GPopt on diabetes data
  • Interpretation of LSBoost’s output using the-teller’s new version, 0.7.0. It’s worth mentioning that LSBoost, which is nonlinear, is interpretable as a linear model wherever its activation functions can be differentiated. This requires some calculus (but no calculus today, hence the-teller :) ).

Installing and importing packages

Install packages from PyPI:

pip install mlsauce
pip install GPopt
pip install the-teller==0.7.0
pip install matplotlib==3.1.3

Python packages for the demo:

import GPopt as gp 
import mlsauce as ms
import numpy as np
import pandas as pd
import seaborn as sns
import teller as tr
import matplotlib.pyplot as plt
import matplotlib.style as style
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split, cross_val_score
from time import time

Objective function to be minimized (for hyperparameter tuning)

# Number of boosting iterations (global variable, dangerous)
n_estimators = 250

def lsboost_cv(X_train, y_train, learning_rate=0.1, 
               n_hidden_features=5, reg_lambda=0.1, 
               dropout=0, tolerance=1e-4, 
               col_sample=1, seed=123):

  estimator = ms.LSBoostRegressor(n_estimators=n_estimators, 
                                   learning_rate=learning_rate,
                                   n_hidden_features=np.int(n_hidden_features), 
                                   reg_lambda=reg_lambda,
                                   dropout=dropout,
                                   tolerance=tolerance,
                                   col_sample=col_sample,
                                   seed=seed, verbose=0)

  return -cross_val_score(estimator, X_train, y_train,
                          scoring='neg_root_mean_squared_error', cv=5, n_jobs=-1).mean()

def optimize_lsboost(X_train, y_train):

  def crossval_objective(x):

    return lsboost_cv(            
      X_train=X_train, 
      y_train=y_train,
      learning_rate=x[0],
      n_hidden_features=np.int(x[1]), 
      reg_lambda=x[2], 
      dropout=x[3],
      tolerance=x[4],
      col_sample=x[5])

  gp_opt = gp.GPOpt(objective_func=crossval_objective, 
                      lower_bound = np.array([0.001, 5, 1e-2, 0.1, 1e-6, 0.5]), 
                      upper_bound = np.array([0.4, 250, 1e4, 0.8, 0.1, 0.999]),
                      n_init=10, n_iter=190, seed=123)    
  return {'parameters': gp_opt.optimize(verbose=2, abs_tol=1e-3), 'opt_object':  gp_opt}

Hyperparameter tuning on diabetes data

In the diabetes dataset, the response is “a quantitative measure of disease progression one year after baseline”. The explanatory variables are:

  • age: age in years

  • sex

  • bmi: body mass index

  • bp: average blood pressure

  • s1: tc, total serum cholesterol

  • s2: ldl, low-density lipoproteins

  • s3: hdl, high-density lipoproteins

  • s4: tch, total cholesterol / HDL

  • s5: ltg, possibly log of serum triglycerides level

  • s6: glu, blood sugar level

# load dataset
dataset = load_diabetes()
X = dataset.data
y = dataset.target

# split data into training test and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=0.1, random_state=13)

# Bayesian optimization for hyperparameters tuning                                                    
res = optimize_lsboost(X_train, y_train)  
res

{'opt_object': <GPopt.GPOpt.GPOpt.GPOpt at 0x7f550e5c5f50>,
 'parameters': (array([1.53620422e-01, 6.20779419e+01, 8.39242559e+02, 1.74212646e-01, 5.48527464e-02, 7.15906433e-01]),
  53.61909741088658)}

Adjusting LSBoost to diabetes data (training set) and obtaining predictions

# _best_ hyperparameters
parameters = res["parameters"][0]

# Adjusting LSBoost to diabetes data (training set)
estimator = ms.LSBoostRegressor(n_estimators=n_estimators,
                                   learning_rate=parameters[0],
                                   n_hidden_features=np.int(parameters[1]), 
                                   reg_lambda=parameters[2], 
                                   dropout=parameters[3],  
                                   tolerance=parameters[4], 
                                   col_sample=parameters[5],
                                   seed=123, verbose=1).fit(X_train, y_train)

# predict on test set
err = estimator.predict(X_test) - y_test
print(f"\n\n Test set RMSE: {np.sqrt(np.mean(np.square(err)))}")

100%|██████████| 250/250 [00:01<00:00, 132.50it/s]

 Test set RMSE: 55.92500853500942

Create an Explainer object in order to understand LSBoost decisions

As a reminder, the-teller computes changes (effects) in the response (variable to be explained), consecutive to a small change in an explanatory variable.

# creating an Explainer object
explainer = tr.Explainer(obj=estimator)

# fitting the Explainer to unseen data
explainer.fit(X_test, y_test, X_names=dataset.feature_names, method="avg")

Heterogeneity of marginal effects:

# heterogeneity because 45 patients in test set => a distribution of effects
explainer.summary() 

           mean         std      median         min         max
bmi  556.001858  198.440761  498.042418  295.134632  877.900389
s5   502.361989   56.518532  488.352521  423.339630  663.398877
bp   256.974826  121.099501  245.205494   83.019164  495.913721
s4   190.995503   69.881801  185.163689   49.870049  356.093240
s6    72.047634  100.701186   76.269634  -68.037669  229.263444
age   55.482125  185.000373   61.218433 -174.677003  329.485983
s2    -8.097623   49.166848  -10.127223  -78.075175  104.572880
s1  -141.735836   72.327037 -115.976202 -292.320955   -6.694544
s3  -146.470803  164.826337 -196.285307 -357.895526  132.102133
sex -234.702770  162.564859 -314.707386 -415.665287   24.017851

Visualizing the average effects (new in version 0.7.0):

explainer.plot(what="average_effects")

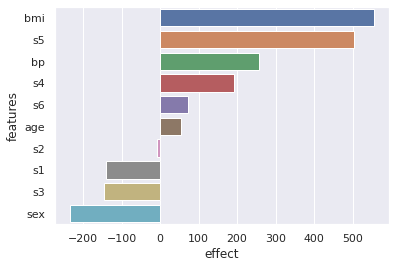
lsboost-explainer-avg

Visualizing the distribution (heterogeneity) of effects (new in version 0.7.0):

explainer.plot(what="hetero_effects")

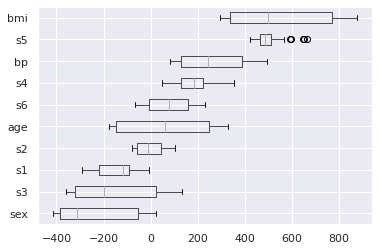
lsboost-explainer-hetero

If you’re interested in obtaining all the individual effects, for each patient, then type:

print(explainer.get_individual_effects())

Comments powered by Talkyard.