This post explores a few configurations of nnetsauce’s Generalized nonlinear models (GNLMs), especially the regularization parameters guarding the model against overfitting. There are many, many other configurations that can be envisaged, which I will do over time. GNLM is still very young and experimental. There’ll be no advanced tuning in this post, but rather an analysis of some hyperparameters, when everything else is held constant (default hyperparameters). Many other examples of use of nnetsauce’s GNLM can be found in the following notebook: thierrymoudiki_040920_examples.ipynb.

Let X be a matrix of explanatory variables for a response y. The general philosophy of GNLMs in the nnetsauce is to minimize a loss function L defined as:

\[\begin{eqnarray*} L &=& loss(y, Z; \beta)\\ &+& \lambda_1 \left( \alpha_1||\beta_1||_1 + \frac{1}{2}(1 - \alpha_1)||\beta_1||_2^2 \right)\\ &+& \lambda_2 \left( \alpha_2||\beta_2||_1 + \frac{1}{2}(1 - \alpha_2)||\beta_2||_2^2 \right)\\ \end{eqnarray*}\]

Z is a transformed version of X; a columnwise concatenation of a standardized X and g(XW+b). g(XW+b)?

  • g is an elementwise activation function, for example \(x \mapsto max(x, 0)\), which makes the whole learning procedure nonlinear.
  • W is drawn from a deterministic Sobol sequence; it helps in creating new, various features from X.
  • b is a bias term.
  • \(\lambda\) and \(\alpha\) both create Elastic Net-like penalties on model coefficients \(\beta\). Typically, they add some bias to the basis loss (loss), so that the GNLMs are able to generalize when dealing with unseen data.

Regarding \(\beta\) now, some of its coefficients are related to X (\(\beta_1\)), and the rest to g(XW+b) (\(\beta_2\)). Examples of \(loss\) functions include (non-exhaustive list):

  • Gaussian:
\[loss(y, Z; \beta) = \frac{1}{2} || y - Z \beta ||_2^2\]
  • Laplace
\[loss(y, Z; \beta) = || y - Z \beta ||_1\]

Ultimately, nnetsauce’s implementation of GNLMs will include other loss functions such as binomial or Poisson likelihoods (…) for count data.

Minimizing L is currently achieved in the nnetsauce by employing stochastic gradient descent and/or stochastic coordinate descent (SCD) (there are certainly other possibilities/choices). In this post, we will use the latter, which is less encountered in the wild. nnetsauce’s implementation of SCD can use only a subsample of the whole dataset at each iteration of the optimizer. A stratified subsampling of y is applied, so that the distribution of y’s subsamples is very close to the distribution of the whole y.

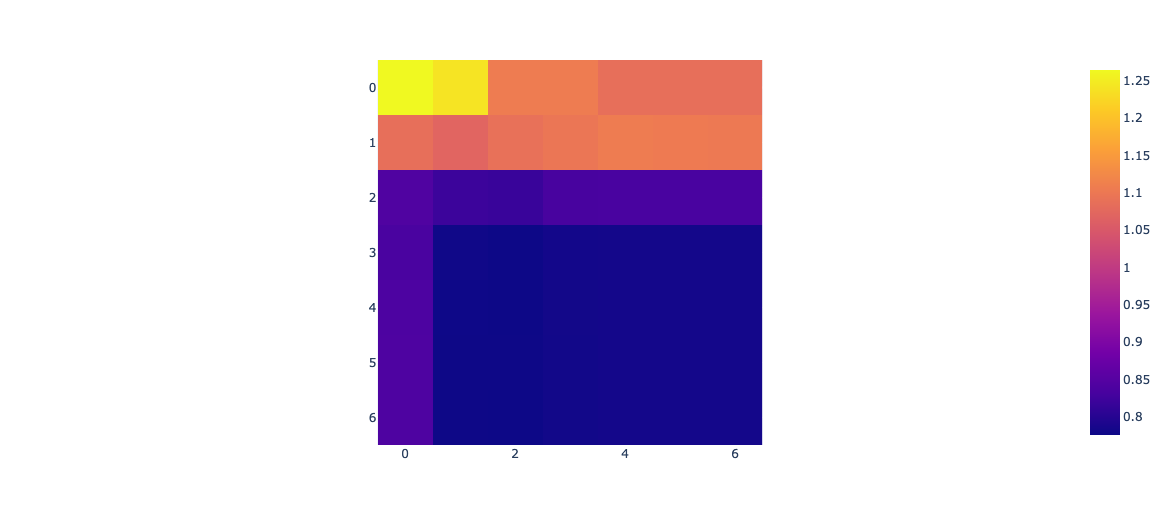
5-fold cross-validation RMSE as function of \(\lambda_1\) and \(\lambda_2\) on 100 observations (California Housing data)

x-axis: \(\lambda_2\), y-axis: \(\lambda_1\); both ranging from 10 to 1e-5 (7 points)

pres-image

5-fold cross-validation RMSE as function of \(\alpha_1\) and \(\alpha_2\) on 100 observations (California Housing data)

x-axis: \(\alpha_2\), y-axis: \(\alpha_1\); both ranging from 0 to 1 (5 points)

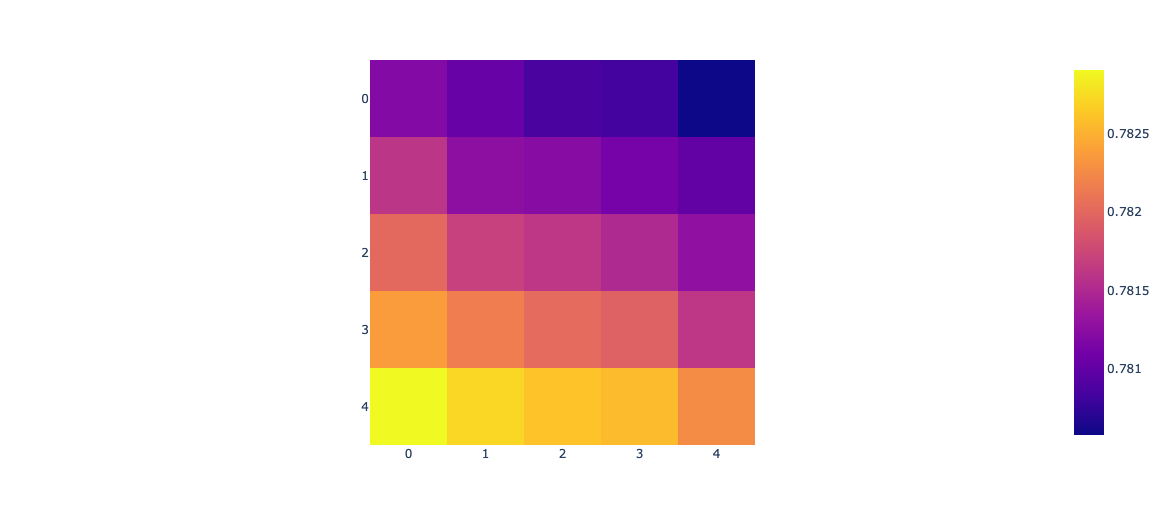
pres-image

All else held constant, to achieve a good performance on this dataset, the model prefers relatively low values of \(\lambda_1\) and \(\lambda_2\). When it comes to choosing \(\alpha\)’s, the following L is preferred:

\[\begin{equation} L = loss(y, Z; \beta) + \lambda_1 \left( \frac{1}{2}||\beta_1||_2^2 \right) + \lambda_2 \left( ||\beta_2||_1 \right) \end{equation}\]

Remember, though, that there are several other interactions with other hyperparameters. So that, it’s better to tune all of them simultaneously.

The code for these graphs (and more) can be found in this notebook.

Comments powered by Talkyard.