A few weeks ago, I introduced a target-based categorical encoder for Statistical/Machine Learning based on correlations + Cholesky decomposition. That is, a way to convert explanatory variables such as the x below, to numerical variables which can be digested by ML models.

# Have:
x <- c("apple", "tomato", "banana", "apple", "pineapple", "bic mac",
	"banana", "bic mac", "quinoa sans gluten", "pineapple", 
	"avocado", "avocado", "avocado", "avocado!", ...)

# Need:
new_x <- c(0, 1, 2, 0, 3, 4, 2, ...)

This week, I use the tips dataset (available here). Imagine that you work in a restaurant, and also have access to the following billing information:

    total_bill   tip     sex smoker   day    time  size
0         16.99  1.01  Female     No   Sun  Dinner     2
1         10.34  1.66    Male     No   Sun  Dinner     3
2         21.01  3.50    Male     No   Sun  Dinner     3
3         23.68  3.31    Male     No   Sun  Dinner     2
4         24.59  3.61  Female     No   Sun  Dinner     4
..          ...   ...     ...    ...   ...     ...   ...
239       29.03  5.92    Male     No   Sat  Dinner     3
240       27.18  2.00  Female    Yes   Sat  Dinner     2
241       22.67  2.00    Male    Yes   Sat  Dinner     2
242       17.82  1.75    Male     No   Sat  Dinner     2
243       18.78  3.00  Female     No  Thur  Dinner     2

[244 rows x 7 columns]

Based on this information, you’d like to understand how to maximize your tip ^^. In a Statistical/Machine Learning model, nnetsauce’s Ridge2Regressor in this post, the response to be understood is the numerical variable tip. The explanatory variables are total_bill, sex, smoker, day, time, size. However, sex, smoker, day, time are not digestible as is; they need to be numerically encoded.

So, if we let df be a data frame containing all the previous information on tips, and pseudo_tip be the pseudo target created as explained in this previous post using R, then by using the querier, a numerical data frame df_numericcan be obtained from df as:

import numpy as np
import pandas as pd
import querier as qr

Z = qr.select(df, 'total_bill, sex, smoker, day, time, size')
df_numeric = pd.DataFrame(np.zeros(Z.shape), 
                               columns=Z.columns)
col_names = Z.columns.values

if (qr.select(Z, col).values.dtype == np.object): # if column is not numerical
                   
    # average a pseudo-target instead of the real response                    
    Z_temp = qr.summarize(df, req = col + ', avg(pseudo_tip)', 
                           group_by = col)
    levels = np.unique(qr.select(Z, col).values)
    
    for l in levels:
        
        qrobj = qr.Querier(Z_temp)
        
        val = qrobj\
              .filtr(col + '== "' + l + '"')\
              .select("avg_pseudo_tip")\
              .df.values
              
        df_numeric.at[np.where(Z[col] == l)[0], col] = np.float(val)
        
else:   
    
    df_numeric[col] = Z[col]

Below on the left, we can observe the distribution of tips, ranging approximately from 1 to 10. On the right, I obtained Ridge2Regressor’s cross-validation root mean squared error (RMSE) for different values of the target correlation (50 repeats each):

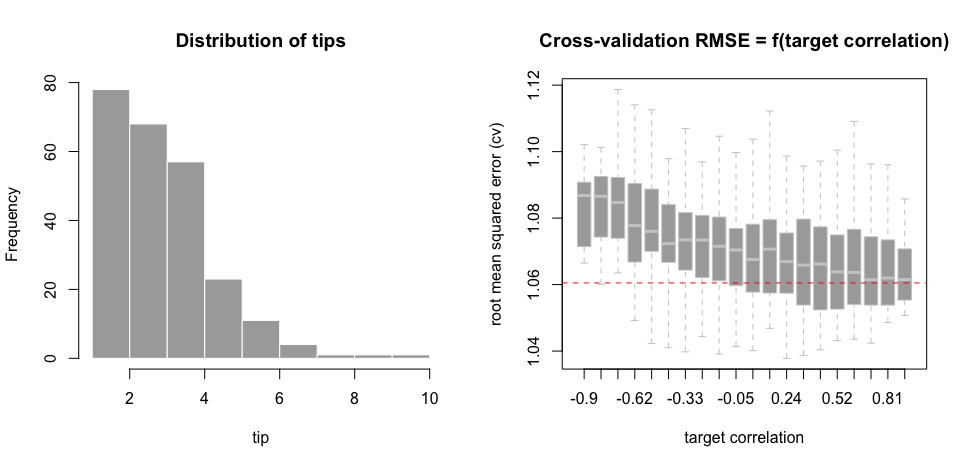
image-title-here

Surprisingly (or not?), the result is not compatible with my intuition. Considering that we are constructing encoded explanatory variables by using the response (a form of subtle overfitting), I was expecting a lower cross-validation error for low target correlations – close to 0 or slightly negative. But the lowest 5-fold cross-validation error is obtained for a target correlation equal to 0.7. It will be interesting to see how these results generalize. Though, it’s worth noticing that accross target correlations, the volatility of Ridge2Regressor cross-validation errors – adjusted with default parameters here – remains low.

More on this later…

Comments powered by Talkyard.